Ex.
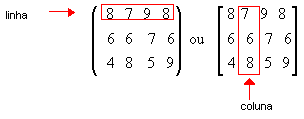
2. Representação genérica de uma matriz: os números de uma matriz são chamados de elementos.
 Deste modo, qualquer matriz pode ser representada da forma: A=(aij)mxn; i esteja entre 1 e m bem como, j esteja entre 1 e n.
Deste modo, qualquer matriz pode ser representada da forma: A=(aij)mxn; i esteja entre 1 e m bem como, j esteja entre 1 e n.3. Igualdade entre matrizes:
Duas matrizes, A e B, do mesmo tipo m x n, são iguais se, e somente se, todos os elementos que ocupam a mesma posição são iguais:
4. Tipos de matriz:
- NOMECARACTERÍSTICAEXEMPLOLinhaPossui apenas 1 linhaA = (2 3 -1 4 )ColunaPossui apenas 1 coluna
 QuadradaPossui a mesma quantidade de linhas e colunas
QuadradaPossui a mesma quantidade de linhas e colunas DiagonalMatriz quadrada que possui os elementos da diagonal principal diferentes de zero e os demais elementos iguais a zero.
DiagonalMatriz quadrada que possui os elementos da diagonal principal diferentes de zero e os demais elementos iguais a zero. IdentidadeMatriz diagonal que possui os elementos da diagonal principal iguais a um e os demais elementos iguais a zero.
IdentidadeMatriz diagonal que possui os elementos da diagonal principal iguais a um e os demais elementos iguais a zero. NulaMatriz que possui todos os elementos iguais a zero
NulaMatriz que possui todos os elementos iguais a zero Triangular SuperiorMatriz quadrada em que os elementos localizados abaixo da diagonal principal são nulos.
Triangular SuperiorMatriz quadrada em que os elementos localizados abaixo da diagonal principal são nulos. Triangular InferiorMatriz quadrada em que os elementos localizados acima da diagonal principal são nulos.
Triangular InferiorMatriz quadrada em que os elementos localizados acima da diagonal principal são nulos.
- matriz transposta:
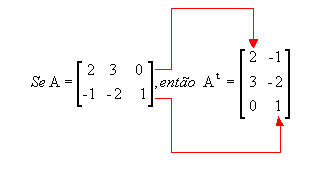
4. Operações com matrizes:
i) Adição:
Dadas as matrizes 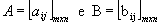 , chamamos de soma dessas matrizes a matriz
, chamamos de soma dessas matrizes a matriz 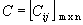 , tal que Cij = aij + bij , para todo
, tal que Cij = aij + bij , para todo 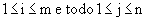 :
:
Ex:A + B = C |
Obs: A + B existe se, e somente se, A e B forem do mesmo tipo.
Propriedades
Sendo A, B e C matrizes do mesmo tipo ( m x n), temos as seguintes propriedades para a adição:
a) comutativa: A + B = B + A
b) associativa: ( A + B) + C = A + ( B + C)
c) elemento neutro: A + 0 = 0 + A = A, sendo 0 a matriz nula m x n
d) elemento oposto: A + ( - A) = (-A) + A = 0
ii) Subtração:
Dadas as matrizes A - B = A + ( - B ) |
Observe:
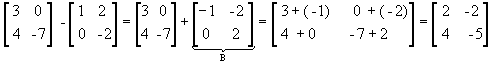
iii) Multiplicação por escalar:
Dados um número real x e uma matriz A do tipo m x n, o produto de x por A é uma matriz Bdo tipo m x n obtida pela multiplicação de cada elemento de A por x, ou seja, bij = xaij:
B = x.A |
Ex:
Propriedades
Sendo A e B matrizes do mesmo tipo ( m x n) e x e y números reais quaisquer, valem as seguintes propriedades:
a) associativa: x . (yA) = (xy) . A
b) distributiva de um número real em relação à adição de matrizes: x . (A + B) = xA + xB
c) distributiva de uma matriz em relação à adição de dois números reais: (x + y) . A = xA + yA
d) elemento neutro : xA = A, para x=1, ou seja, A=A
iv) Multiplicação de matrizes:
O produto de uma matriz por outra não é determinado por meio do produto dos sus respectivos elementos.
Assim, o produto das matrizes A = ( aij) m x p e B = ( bij) p x n é a matriz C = (cij) m x n em que cada elemento cij é obtido por meio da soma dos produtos dos elementos correspondentes da i-ésima linha de A pelos elementos da j-ésima coluna B.
Ex:
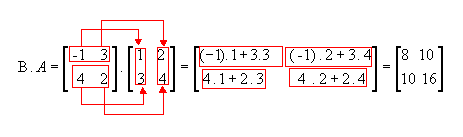
Portanto, 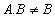 .A, ou seja, para a multiplicação de matrizes não vale a propriedade comutativa.
.A, ou seja, para a multiplicação de matrizes não vale a propriedade comutativa.
Da definição, temos que a matriz produto A . B só existe se o número de colunas de A for igual ao número de linhas de B:
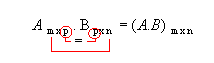
A matriz produto terá o número de linhas de A (m) e o número de colunas de B(n):
- Se A3 x 2 e B 2 x 5 , então ( A . B ) 3 x 5
- Se A 4 x 1 e B 2 x 3, então não existe o produto
- Se A 4 x 2 e B 2 x 1, então ( A . B ) 4 x 1
Propriedades
Verificadas as condições de existência para a multiplicação de matrizes, valem as seguintes propriedades:
a) associativa: ( A . B) . C = A . ( B . C )
b) distributiva em relação à adição: A . ( B + C ) = A . B + A . C ou ( A + B ) . C = A . C + B . C
c) elemento neutro: A . In = In . A = A, sendo In a matriz identidade de ordem n
Vimos que a propriedade comutativa, geralmente, não vale para a multiplicação de matrizes. Não vale também o anulamento do produto, ou seja: sendo 0 m x n uma matriz nula, A .B =0 m x n não implica, necessariamente, que A = 0 m x n ou B = 0 m x n.
5. Matriz inversa:
Dada uma matriz A, quadrada, de ordem n, se existir uma matriz A', de mesma ordem, tal que A . A' = A' . A = In , então A' é matriz inversa de A . representamos a matriz inversa por A-1 .
A.B = B.A = I
6. Equações matriciais: são equações em que a incógnita é uma matriz
7. Determinantes:
- Determinante de 2ª ordem
 , de ordem 2, por definição o determinante associado a M, determinante de 2ª ordem, é dado por:
, de ordem 2, por definição o determinante associado a M, determinante de 2ª ordem, é dado por: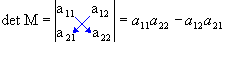
Portanto, o determinante de uma matriz de ordem 2 é dado pela diferença entre o produto dos elementos da diagonal principal e o produto dos elementos da diagonal secundária. Veja o exemplo a seguir.
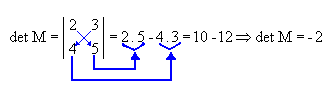
- Regra de Sarrus
O cálculo do determinante de 3ª ordem pode ser feito por meio de um dispositivo prático, denominado regra de Sarrus.
Acompanhe como aplicamos essa regra para 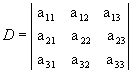 .
.
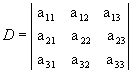 .
.1º passo: Repetimos as duas primeiras colunas ao lado da terceira:
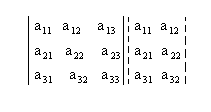
2º passo: Encontramos a soma do produto dos elementos da diagonal principal com os dois produtos obtidos pela multiplicação dos elementos das paralelas a essa diagonal (a soma deve ser precedida do sinal positivo):
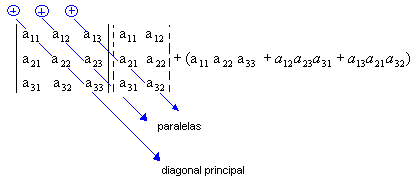
3º passo: Encontramos a soma do produto dos elementos da diagonal secundária com os dois produtos obtidos pela multiplicação dos elementos das paralelas a essa diagonal ( a soma deve ser precedida do sinal negativo):
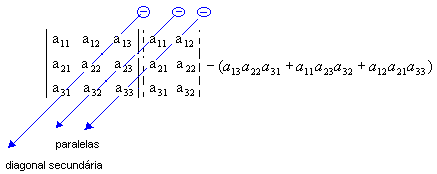

Propriedades dos determinantes
Os demais associados a matrizes quadradas de ordem n apresentam as seguintes propriedades:
P1 ) Quando todos os elementos de uma fila ( linha ou coluna) são nulos, o determinante dessa matriz é nulo.
Exemplo:
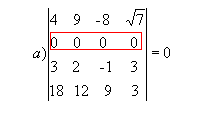 | 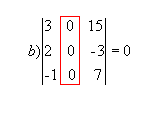 |
P2) Se duas filas de uma matriz são iguais, então seu determinante é nulo.
Exemplo:
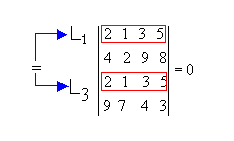
P3) Se duas filas paralelas de uma matriz são proporcionais, então seu determinante é nulo.
Exemplo:
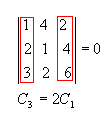
P4) Se os elementos de uma fila de uma matriz são combinações lineares dos elementos correspondentes de filas paralelas, então seu determinante é nulo.
Exemplos:
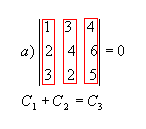 | 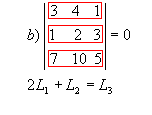 |
P5 ) Teorema de Jacobi: o determinante de uma matriz não se altera quando somamos aos elementos de uma fila uma combinação linear dos elementos correspondentes de filas paralelas.
Exemplo:
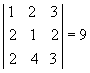
Substituindo a 1ª coluna pela soma dessa mesma coluna com o dobro da 2ª, temos:
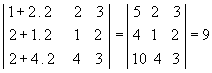
P6) O determinante de uma matriz e o de sua transposta são iguais.
Exemplo:
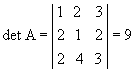 | 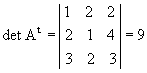 |
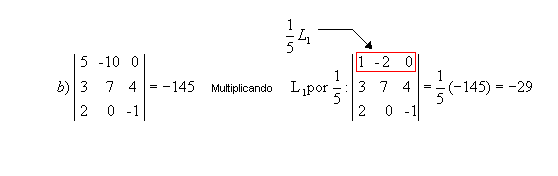
Exemplos:
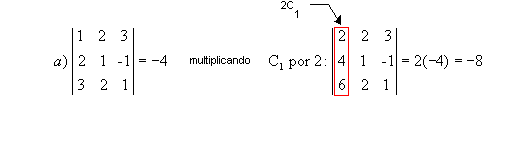 |
 |
Exemplo:
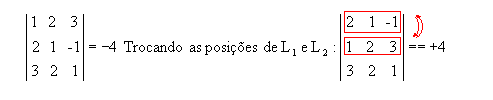
P9) Quando, em uma matriz, os elementos acima ou abaixo da diagonal principal são todos nulos, o determinante é igual ao produto dos elementos dessa diagonal.
Exemplos:
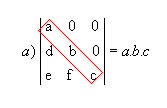 | 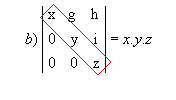 |
- Menor complementar
Chamamos de menor complementar relativo a um elemento aij de uma matriz M, quadrada e de ordem n>1, o determinante MCij , de ordem n - 1, associado à matriz obtida de M quando suprimimos a linha e a coluna que passam por aij .
Vejamos como determiná-lo pelos exemplos a seguir:
a) Dada a matriz  , de ordem 2, para determinar o menor complementar relativo ao elemento a11(MC11), retiramos a linha 1 e a coluna 1:
, de ordem 2, para determinar o menor complementar relativo ao elemento a11(MC11), retiramos a linha 1 e a coluna 1:
 , de ordem 2, para determinar o menor complementar relativo ao elemento a11(MC11), retiramos a linha 1 e a coluna 1:
, de ordem 2, para determinar o menor complementar relativo ao elemento a11(MC11), retiramos a linha 1 e a coluna 1: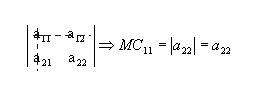
Da mesma forma, o menor complementar relativo ao elemento a12 é:
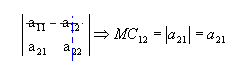
b) Sendo  , de ordem 3, temos:
, de ordem 3, temos:
Cofator , de ordem 3, temos:
, de ordem 3, temos:Chamamos de cofator ou complemento algébrico relativo a um elemento aij de uma matriz quadrada de ordem n o número Aij tal que Aij = (-1)i+j . MCij .
Veja:
a) Dada
 , os cofatores relativos aos elementos a11 e a12 da matriz M são:
, os cofatores relativos aos elementos a11 e a12 da matriz M são: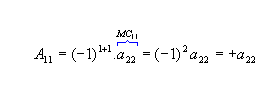 | 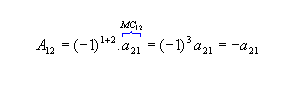 |
b) Sendo  , vamos calcular os cofatores A22, A23 e A31:
, vamos calcular os cofatores A22, A23 e A31:
 , vamos calcular os cofatores A22, A23 e A31:
, vamos calcular os cofatores A22, A23 e A31: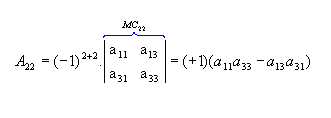 |
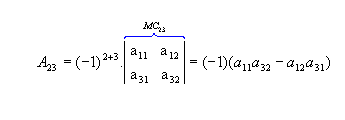 |
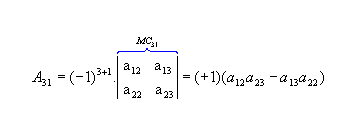 |
Teorema de Laplace
O determinante de uma matriz quadrada M = [aij]mxn 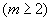 pode ser obtido pela soma dos produtos dos elementos de uma fila qualquer ( linha ou coluna) da matriz M pelos respectivos cofatores.
pode ser obtido pela soma dos produtos dos elementos de uma fila qualquer ( linha ou coluna) da matriz M pelos respectivos cofatores.
Assim, fixando 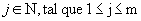 , temos:
, temos:
em que 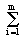 é o somatório de todos os termos de índice i, variando de 1 até m,
é o somatório de todos os termos de índice i, variando de 1 até m, 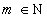 .
.
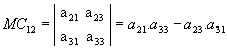
Nenhum comentário:
Postar um comentário